
こちらのサイトと本に影響されて考え始めたネタですが...
前回のメモではあまりにわけわかめなので、肝となるNAND恒等式を実現する歯車機構を単純化して描画してみました。
"恒等式"というのが肝です。
| NAND(0,0)≡1 | NAND(1,0)≡1 | NAND(0,1)≡1 | NAND(1,1)≡0 |
 |
 |
 |
 |
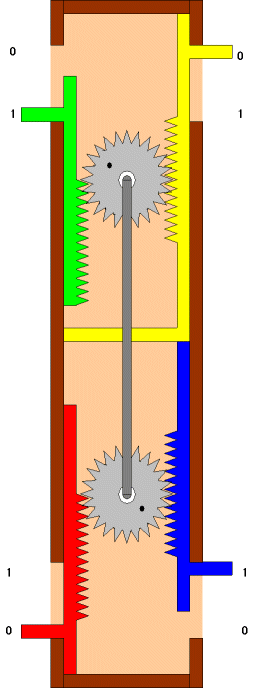
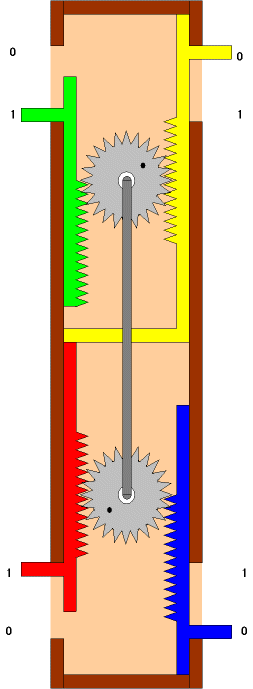
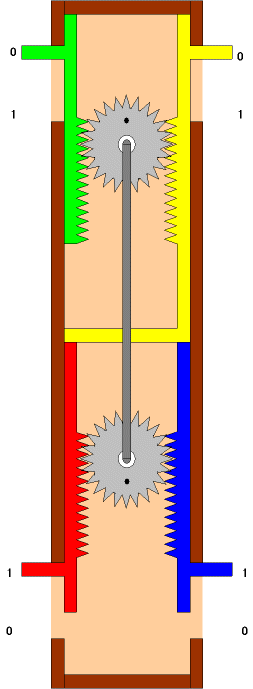
青/赤のギアがそれぞれ通常のNANゲートで言うところの入力(この場合入力も出力も無いのですが)、緑のギアが出力です。
NANDゲートの取りうる4状態を示しています。 青/赤ともに、0の場合は、緑は1です。この状態から、赤、又は、緑の片方だけ上(1)に押し上げようとした場合、黄色いギヤが引き上げられる為、赤や緑には力が掛かりません。この機構は、赤、青、緑にどのように力を加えても、恒にNANDの関係を崩すことなく、状態遷移の力が他の端子に均等に伝わります。入力と出力という概念がありません。純粋に3ポートが公平に相互作用する機構です。
さてここで、もしこの論理素子を大量に繋げて、論理回路を構成した場合どうなるか?
というのがテーマです。
私の予想ですが、恐らくまず、挙動の正確な解をチューリングマシンで計算することは出来ません。3体問題みたいなもんです。数式に置けないはずです(時間を掛ければ近似解を得るシュミレーションは可能とは思いますが)。
次に、あらゆる演算の逆方向の演算が可能になると考えます。
即ち答えから、その答えになりうる入力パラメータが求められると考えられます。
答えの出てくるポートの論理を固定した場合、恒等式の特性から、関数パラメータ側の値は、その答えを導く値の集合のウチの何れかしか取れなくなると考えます。
ぶっちゃけ、乗算器を構成すれば、素因数分解が可能になり、量子コンピュータを待たずに暗号破りが出来ます(笑)。
また、NP完全問題でおなじみの、巡回セールスマン問題やナップザック問題なども解けるかもしれません。
「グラフ」と「順列」を入力すると、「道程の長さ」を出力する回路を作ります。
そして、グラフを入力し、値を固定します。
次に、「道程の長さ」のMSB(上位ビット)から順に0方向に壊れない程度の力で引っ張り、0に移動できたらそこで固定、出来なければ1のまま固定という操作を繰り返します。
すると、順列のポートには、最短経路を通る順列しか取り得なくなるのではないかと予想できます。
どうでしょう? 思いっきりトンでも科学突入の一歩手前ですね(笑)。
シミュレーション困難なのと、「大量のギアを回しても大丈夫なぐらい丈夫で且、遊びの無いギアが作れるのか?」という問題をクリアしない限り、証明も反証もできない気がします(それって科学になってなひ)。
とりあえず家内制手工業ではどないもなりません(求むスポンサーwww)。
なんとか、電気回路で等価なものが作れないものでしょうか???。