前回のNANDの恒等式の電子回路化を考えつづけて、突然いいアイデアが浮かんだので話を進めていきます。
ギアにおける作用反作用を電気回路でどう表すかが課題でした。逆向きの演算回路でフィードバックというか自己参照ループを組めばいいような気もしていたのですが、単純に戻しただけでは、信号衝突がうまく扱えません。また、能動素子を通す時点で、インピーダンス変換されてしまうのでギアにおける、強い力/弱い力の相互作用が素子を超えて起こせないとずっと思い込んでいました。
が、とあるひらめきで次のような回路を想定してみました。
まずは最も簡単なところで、NOTの恒等式を実現しようとしています。
ポイントは、OPアンプの出力部分に抵抗をいれるというただそれだけ。

で、上のように3段つないで、信号の強弱(つまりはインピーダンス)を見るために、双方向から異なる出力インピーダンスの信号をいれて適当に揺さぶって見ます(とりあえず正弦波を入れてみた)。
以前買ったPSpiceの入門本の体験版でシミュレーションしてみたのが以下です。
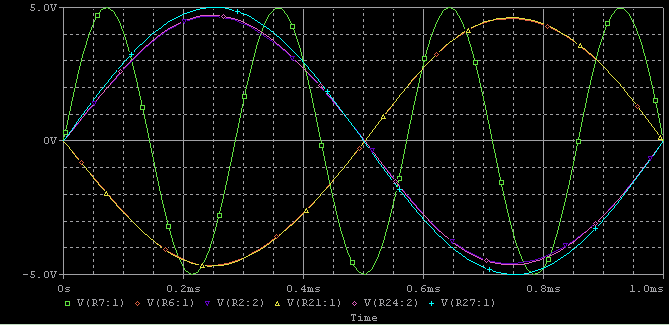
回路図のプローブの色がそのまま波形の色に対応しています。
右から入れている強い信号(低インピーダンス)の信号が全体を支配し、弱い信号(高インピーダンス)が駆逐されているのが分かるかと思います。
動作自体は机上で見てもらっても納得と思います。
で、インバータでいけるなら、差動出力回路にもいけるだろうというのが次のネタで、これも実はうまくいけそうです。
以下、差動出力回路の出力を差動増幅回路でループさせるというものです。
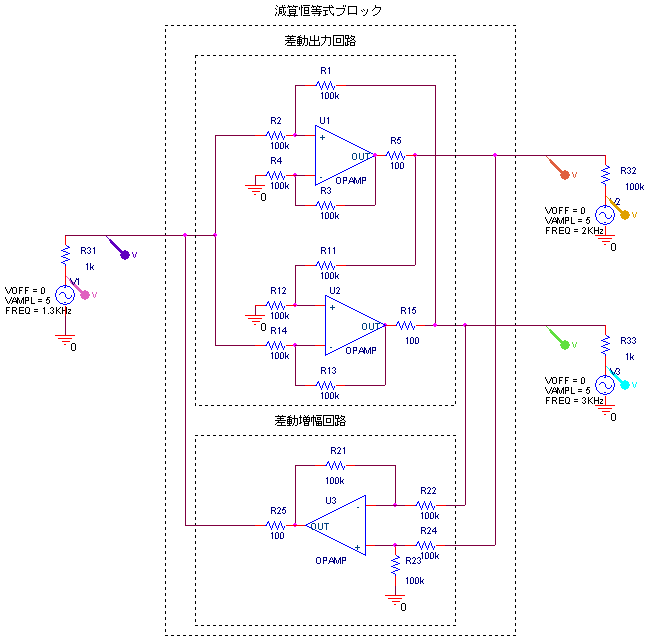
これに関しては、PSpiceが体験版で、これ以上パーツが置けないので今のところ1ブロックで打ち止めです。
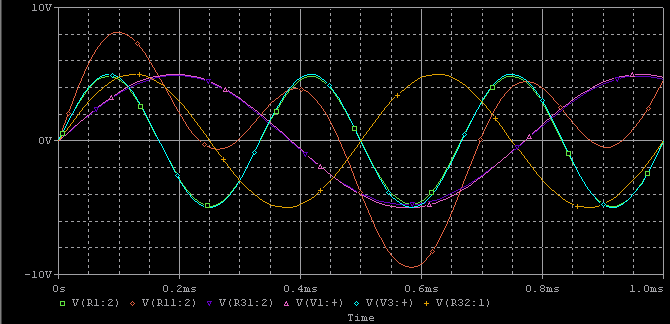
3端子のうち、一つを弱い力で振り回していますが、ドライブの弱いところが負けて、強いところが網を支配しています。
くどいようですが、信号強度と過渡状態をざっぱに可視化するのために正弦波で振ってるだけです(目的はあくまでデジタル的な解で、最後に入れたいのは0と1に対応する電圧です)。
いずれにしろ A-B≡C という恒等式を維持しています。
「ドライブの弱いところが負ける」という事象自体、入力している信号強度より、回路から逆流してくる出力信号の方が強いってことですから、端子間で信号強度(というか信号インピーダンス)が伝播していることが伺えます。
ここまでくれば、例のNANDゲートのギアを電気回路化するのが見えてきました。
ギアのつっかえ棒のところも単なるダイオード(笑)でいけそうです。
NP完全問題を一瞬で解く回路にまた一歩近づいたか?
(というかいろんな暗号が解けてしまふ....)
これらの素子を使って巨大回路を組んだ場合、回路としては過渡状態の多数の素子の入出力が喧嘩し合って、落ち着き先を探すわけですから、ある意味、超並列計算機ともいえます。
この回路を見た先輩曰く「喧嘩サーキットと名づけよう!」。
目指しているのはあくまで「デジタル解」です。入力も出力も0/1だし、解も一意に定まることを目的としています。ただ計算の途中にアナログ的要素を使って解探索を高速化しようという試みです。
まあ、量子コンピュータも状態を重ね合わせることで似たような特性な気もしなくもありません(4端子素子だし)。が、私のお遊びは個人のお遊びレベルで試行錯誤できる分面白いかと。でわでわ。